Predicted Scores in Stata
As we discussed in class, the predicted value of the outcome variable can be created using the regression model. For example, we can use the auto dataset from Stata to look at the relationship between miles per gallon and weight across various cars. We estimate the follow equation
sysuse auto
regress mpg weight
Source | SS df MS Number of obs = 74
-------------+------------------------------ F( 1, 72) = 134.62
Model | 1591.9902 1 1591.9902 Prob > F = 0.0000
Residual | 851.469256 72 11.8259619 R-squared = 0.6515
-------------+------------------------------ Adj R-squared = 0.6467
Total | 2443.45946 73 33.4720474 Root MSE = 3.4389
------------------------------------------------------------------------------
mpg | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
weight | -.0060087 .0005179 -11.60 0.000 -.0070411 -.0049763
_cons | 39.44028 1.614003 24.44 0.000 36.22283 42.65774
------------------------------------------------------------------------------
Thus, we see a negative relationship between weight and mpg. For every 1 unit increase in weight, mpg goes down by -.006. We can obtain the predicted scores for the observations in our dataset with the following command:
predict mpg_pred
This creates a new variable called mpg_pred with the predicted mpg for all the weight values in our dataset. Here’s 20 of the actual mpg values and 20 of the predicted values.
list mpg mpg_pred in 1/20
+----------------+
| mpg mpg_pred |
|----------------|
1. | 22 21.83483 |
2. | 17 19.31118 |
3. | 22 23.57735 |
4. | 20 19.91205 |
5. | 15 14.92484 |
|----------------|
6. | 18 17.3884 |
7. | 26 26.04091 |
8. | 20 19.73179 |
9. | 16 16.12658 |
10. | 19 19.01075 |
|----------------|
11. | 14 13.42267 |
12. | 14 16.0064 |
13. | 21 13.66302 |
14. | 29 26.76196 |
15. | 16 17.26823 |
|----------------|
16. | 22 20.33266 |
17. | 22 20.09231 |
18. | 24 22.9164 |
19. | 19 18.83049 |
20. | 30 26.70187 |
+----------------+
Residuals in Stata
Recall the a residual in regression is defined as the difference between the actual value of and the predicted value of
(or
):
Thus, to compute residuals we can just subtract mpg_pred from mpg. Stata will do this for us using the predict command:
predict mpg_res, residuals
Here’s 20 of the actual mpg values, 20 of the predicted values, and 20 of the residuals.
list mpg mpg_pred mpg_res in 1/20
+----------------------------+
| mpg mpg_pred mpg_res |
|----------------------------|
1. | 22 21.83483 .1651688 |
2. | 17 19.31118 -2.311183 |
3. | 22 23.57735 -1.57735 |
4. | 20 19.91205 .0879486 |
5. | 15 14.92484 .0751587 |
|----------------------------|
6. | 18 17.3884 .6115971 |
7. | 26 26.04091 -.0409119 |
8. | 20 19.73179 .2682092 |
9. | 16 16.12658 -.1265787 |
10. | 19 19.01075 -.0107484 |
|----------------------------|
11. | 14 13.42267 .5773304 |
12. | 14 16.0064 -2.006405 |
13. | 21 13.66302 7.336983 |
14. | 29 26.76196 2.238046 |
15. | 16 17.26823 -1.268229 |
|----------------------------|
16. | 22 20.33266 1.667341 |
17. | 22 20.09231 1.907688 |
18. | 24 22.9164 1.083605 |
19. | 19 18.83049 .1695122 |
20. | 30 26.70187 3.298132 |
+----------------------------+
We can see that the residuals are intact the difference between the first two columns.
Given that the residuals are the part of the mpg that is unrelated to weight, mpg_res should be uncorrelated with weight. Let’s check:
. corr weight mpg_res
(obs=74)
| weight mpg_res
-------------+------------------
weight | 1.0000
mpg_res | 0.0000 1.0000
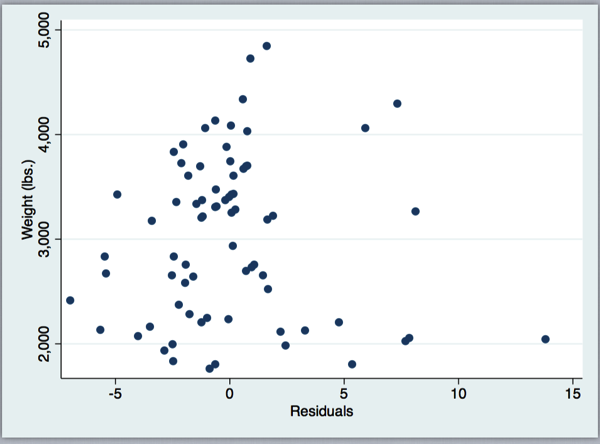
Magic!